Data Management with Postgres (PostGIS)

1. OGC Geometry

The Open Geospatial Consortium (OGC) developed the Simple Features Access standard (SFA) to provide a model for geospatial data. It defines the fundamental spatial type of Geometry, along with operations which manipulate and transform geometry values to perform spatial analysis tasks. PostGIS implements the OGC Geometry model as the PostgreSQL data types geometry and geography.

Geometry is an abstract type. Geometry values belong to one of its concrete subtypes which represent various kinds and dimensions of geometric shapes. These include the atomic types Point, LineString, LinearRing and Polygon, and the collection types MultiPoint, MultiLineString, MultiPolygon and GeometryCollection.

Geometry models shapes in the 2-dimensional Cartesian plane. The PolyhedralSurface, Triangle, and TIN types can also represent shapes in 3-dimensional space. The size and location of shapes are specified by their coordinates. Each coordinate has a X and Y ordinate value determining its location in the plane. Shapes are constructed from points or line segments, with points specified by a single coordinate, and line segments by two coordinates.

Coordinates may contain optional Z and M ordinate values. The Z ordinate is often used to represent elevation. The M ordinate contains a measure value, which may represent time or distance. If Z or M values are present in a geometry value, they must be defined for each point in the geometry. If a geometry has Z or M ordinates the coordinate dimension is 3D; if it has both Z and M the coordinate dimension is 4D.

Geometry values are associated with a spatial reference system indicating the coordinate system in which it is embedded. The spatial reference system is identified by the geometry SRID number. The units of the X and Y axes are determined by the spatial reference system. In planar reference systems the X and Y coordinates typically represent easting and northing, while in geodetic systems they represent longitude and latitude. SRID 0 represents an infinite Cartesian plane with no units assigned to its axes.

The geometry dimension is a property of geometry types. Point types have dimension 0, linear types have dimension 1, and polygonal types have dimension 2. Collections have the dimension of the maximum element dimension.

A geometry value may be empty. Empty values contain no vertices (for atomic geometry types) or no elements (for collections).

An important property of geometry values is their spatial extent or bounding box, which the OGC model calls envelope. This is the 2 or 3-dimensional box which encloses the coordinates of a geometry. It is an efficient way to represent a geometry’s extent in coordinate space and to check whether two geometries interact.

The geometry model allows evaluating topological spatial relationships. To support this the concepts of interior, boundary and exterior are defined for each geometry type. Geometries are topologically closed, so they always

contain their boundary. The boundary is a geometry of dimension one less than that of the geometry itself.

The OGC geometry model defines validity rules for each geometry type. These rules ensure that geometry values represents realistic situations (e.g. it is possible to specify a polygon with a hole lying outside the shell, but this makes no sense geometrically and is thus invalid). PostGIS also allows storing and manipulating invalid geometry values. This allows detecting and fixing them if needed.

1.1 Point

A Point is a 0-dimensional geometry that represents a single location in coordinate space.

---------------------------

POINT (1 2)

POINT Z (1 2 3)

POINT ZM (1 2 3 4)

---------------------------

1.2 LineString

A LineString is a 1-dimensional line formed by a contiguous sequence of line segments. Each line segment is defined by two points, with the end point of one segment forming the start point of the next segment. An OGC-valid LineString has either zero or two or more points, but PostGIS also allows single-point LineStrings. LineStrings may cross themselves (self-intersect). A LineString is closed if the start and end points are the same. A LineString is simple if it does not self-intersect.

--------------------------------------

LINESTRING (1 2, 3 4, 5 6)

--------------------------------------

1.3 LinearRing

A LinearRing is a LineString which is both closed and simple. The first and last points must be equal, and the line must not self-intersect.

--------------------------------------------------------------

LINEARRING (0 0 0, 4 0 0, 4 4 0, 0 4 0, 0 0 0)

--------------------------------------------------------------

1.4 Polygon

A Polygon is a 2-dimensional planar region, delimited by an exterior boundary (the shell) and zero or more interior boundaries (holes). Each boundary is a LinearRing.

------------------------------------------------------------------------------------------------

POLYGON ((0 0 0,4 0 0,4 4 0,0 4 0,0 0 0),(1 1 0,2 1 0,2 2 0,1 2 0,1 1 0))

------------------------------------------------------------------------------------------------

1.5 MultiPoint

A MultiPoint is a collection of Points.

-------------------------------------

MULTIPOINT ( (0 0), (1 2) )

-------------------------------------

1.6 MultiLineString

A MultiLineString is a collection of LineStrings. A MultiLineString is closed if each of its elements is closed.

-----------------------------------------------------------------

MULTILINESTRING ( (0 0,1 1,1 2), (2 3,3 2,5 4) )

-----------------------------------------------------------------

1.7 MultiPolygon

A MultiPolygon is a collection of non-overlapping, non-adjacent Polygons. Polygons in the collection may touch only at a finite number of points.

--------------------------------------------------------------------------------------

MULTIPOLYGON (((1 5, 5 5, 5 1, 1 1, 1 5)), ((6 5, 9 1, 6 1, 6 5)))

--------------------------------------------------------------------------------------

1.8 GeometryCollection

A GeometryCollection is a heterogeneous (mixed) collection of geometries.

----------------------------------------------------------------------------------------

GEOMETRYCOLLECTION ( POINT(2 3), LINESTRING(2 3, 3 4))

----------------------------------------------------------------------------------------

1.9 PolyhedralSurface

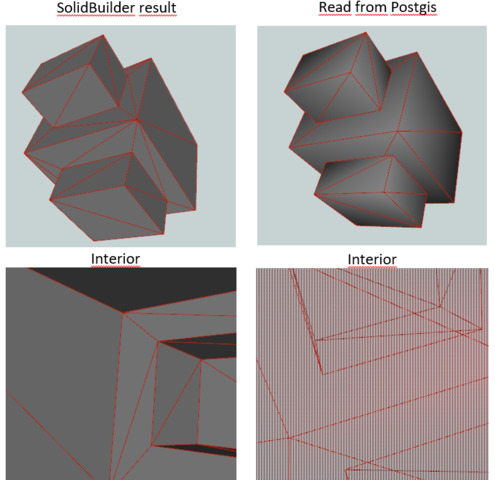
A PolyhedralSurface is a contiguous collection of patches or facets which share some edges. Each patch is a planar Polygon. If the Polygon coordinates have Z ordinates then the surface is 3-dimensional.

------------------------------------------------------------------------------------

POLYHEDRALSURFACE Z (((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)),

((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)),

((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),

((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)),

((0 1 0, 0 1 1, 1 1 1, 1 1 0, 0 1 0)),

((0 0 1, 1 0 1, 1 1 1, 0 1 1, 0 0 1)) )

-------------------------------------------------------------------------------------

1.10 Triangle

A Triangle is a polygon defined by three distinct non-collinear vertices. Because a Triangle is a polygon it is specified by four coordinates, with the first and fourth being equal.

------------------------------------------

TRIANGLE ((0 0, 0 9, 9 0, 0 0))

------------------------------------------

1.11 TIN

A TIN is a collection of non-overlapping Triangles representing a Triangulated Irregular Network.

-------------------------------------------------------------------------------------

TIN Z ( ((0 0 0, 0 0 1, 0 1 0, 0 0 0)), ((0 0 0, 0 1 0, 1 1 0, 0 0 0)) )

-------------------------------------------------------------------------------------

2. SQL/MM Part 3 - Curves

The ISO/IEC 13249-3 SQL Multimedia - Spatial standard (SQL/MM) extends the OGC SFA to define Geometry subtypes containing curves with circular arcs. The SQL/MM types support 3DM, 3DZ and 4D coordinates.

============================================================================================

All floating point comparisons within the SQL-MM implementation are performed to a specified tolerance, currently 1E-8.

============================================================================================

2.1 CircularString

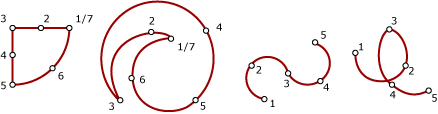
CircularString is the basic curve type, similar to a LineString in the linear world. A single arc segment is specified by three points: the start and end points (first and third) and some other point on the arc. To specify a closed circle the start and end points are the same and the middle point is the opposite point on the circle diameter (which is the center of the arc). In a sequence of arcs the end point of the previous arc is the start point of the next arc, just like the segments of a LineString. This means that a CircularString must have an odd number of points greater than 1.

--------------------------------------------------------

CIRCULARSTRING(0 0, 1 1, 1 0)

CIRCULARSTRING(0 0, 4 0, 4 4, 0 4, 0 0)

--------------------------------------------------------

2.2 CompoundCurve

A CompoundCurve is a single continuous curve that may contain both circular arc segments and linear segments. That means that in addition to having well-formed components, the end point of every component (except the last) must be coincident with the start point of the following component.

----------------------------------------------------------------------------------------

COMPOUNDCURVE( CIRCULARSTRING(0 0, 1 1, 1 0),(1 0, 0 1))

-----------------------------------------------------------------------------------------

2.3 CurvePolygon

A CurvePolygon is like a polygon, with an outer ring and zero or more inner rings. The difference is that a ring can be a CircularString or CompoundCurve as well as a LineString. As of PostGIS 1.4 PostGIS supports compound curves in a curve polygon.

-----------------------------------------------------------

CURVEPOLYGON(

CIRCULARSTRING(0 0, 4 0, 4 4, 0 4, 0 0),

(1 1, 3 3, 3 1, 1 1) )

-----------------------------------------------------------

Example: A CurvePolygon with the shell defined by a CompoundCurve containing a CircularString and a LineString, and a hole defined by a CircularString

---------------------------------------------------------------------------------------

CURVEPOLYGON(

COMPOUNDCURVE( CIRCULARSTRING(0 0,2 0, 2 1, 2 3, 4 3),

(4 3, 4 5, 1 4, 0 0)),

CIRCULARSTRING(1.7 1, 1.4 0.4, 1.6 0.4, 1.6 0.5, 1.7 1) )

-------------------------------------------------------------------------------------

2.4 MultiCurve

A MultiCurve is a collection of curves which can include LineStrings, CircularStrings or CompoundCurves.

---------------------------------------------------------------------------------

MULTICURVE( (0 0, 5 5), CIRCULARSTRING(4 0, 4 4, 8 4))

----------------------------------------------------------------------------------

2.5 MultiSurface

A MultiSurface is a collection of surfaces, which can be (linear) Polygons or CurvePolygons.

------------------------------------------------------------------------------------

MULTISURFACE(

CURVEPOLYGON(

CIRCULARSTRING( 0 0, 4 0, 4 4, 0 4, 0 0),

(1 1, 3 3, 3 1, 1 1)),

((10 10, 14 12, 11 10, 10 10), (11 11, 11.5 11, 11 11.5, 11 11)))

------------------------------------------------------------------------------------

3. WKT and WKB

The OGC SFA specification defines two formats for representing geometry values for external use: Well-Known Text (WKT) and Well-Known Binary (WKB). Both WKT and WKB include information about the type of the object and the coordinates which define it.Well-Known Text (WKT) provides a standard textual representation of spatial data. Examples of WKT representations of spatial objects are:

• POINT(0 0)

• POINT Z (0 0 0)

• POINT ZM (0 0 0 0)

• POINT EMPTY

• LINESTRING(0 0,1 1,1 2)

• LINESTRING EMPTY

• POLYGON((0 0,4 0,4 4,0 4,0 0),(1 1, 2 1, 2 2, 1 2,1 1))

• MULTIPOINT((0 0),(1 2))

• MULTIPOINT Z ((0 0 0),(1 2 3))

• MULTIPOINT EMPTY

• MULTILINESTRING((0 0,1 1,1 2),(2 3,3 2,5 4))

• MULTIPOLYGON(((0 0,4 0,4 4,0 4,0 0),(1 1,2 1,2 2,1 2,1 1)), ((-1 -1,-1 -2,-2 -2,-2 -1,-1 -1)))

• GEOMETRYCOLLECTION(POINT(2 3),LINESTRING(2 3,3 4))

• GEOMETRYCOLLECTION EMPTY

Input and output of WKT is provided by the functions ST_AsText and ST_GeomFromText:

-------------------------------------------

text WKT = ST_AsText(geometry);

geometry = ST_GeomFromText(text WKT, SRID);

--------------------------------------------

For example, a statement to create and insert a spatial object from WKT and a SRID is:

----------------------------------------------------------------

INSERT INTO geotable ( geom, name )

VALUES ( ST_GeomFromText('POINT(-126.4 45.32)', 312), 'A Place');

------------------------------------------------------------------

Well-Known Binary (WKB) provides a portable, full-precision representation of spatial data as binary data (arrays of bytes).Examples of the WKB representations of spatial objects are:

• WKT: POINT(1 1)

    WKB: 0101000000000000000000F03F000000000000F03

• WKT: LINESTRING (2 2, 9 9)

    WKB: 0102000000020000000000000000000040000000000000004000000000000022400000000000002240

Input and output of WKB is provided by the functions ST_AsBinary and ST_GeomFromWKB:

-------------------------------------------

bytea WKB = ST_AsBinary(geometry);

geometry = ST_GeomFromWKB(bytea WKB, SRID);

--------------------------------------------

For example, a statement to create and insert a spatial object from WKB is:

-----------------------------------------------------------------------------------------

INSERT INTO geotable ( geom, name )

VALUES ( ST_GeomFromWKB('\x0101000000000000000000f03f000000000000f03f', 312), 'A Place');

-----------------------------------------------------------------------------------------

Powered by Froala Editor